Polynomial Jnterpolation

Interpolation

NB, this is mostly just me trying out getting plot and org mode to mesh nicely.

Following: https://ece.uwaterloo.ca/~dwharder/NumericalAnalysis/05Interpolation/

Goal: fit a of degree \(n-1\) polynomial to \(n\) points.

Vandermonde

Idea: different powers of \(x\) are linearly independent, so we can solve a system of equations to get the fit (as long as they are unique).

VM =: {:"1 %. {."1 ^/ i.@#
tvm =: {:"1 -: VM p."_ 0/ {."1 NB. check that the result fits the points

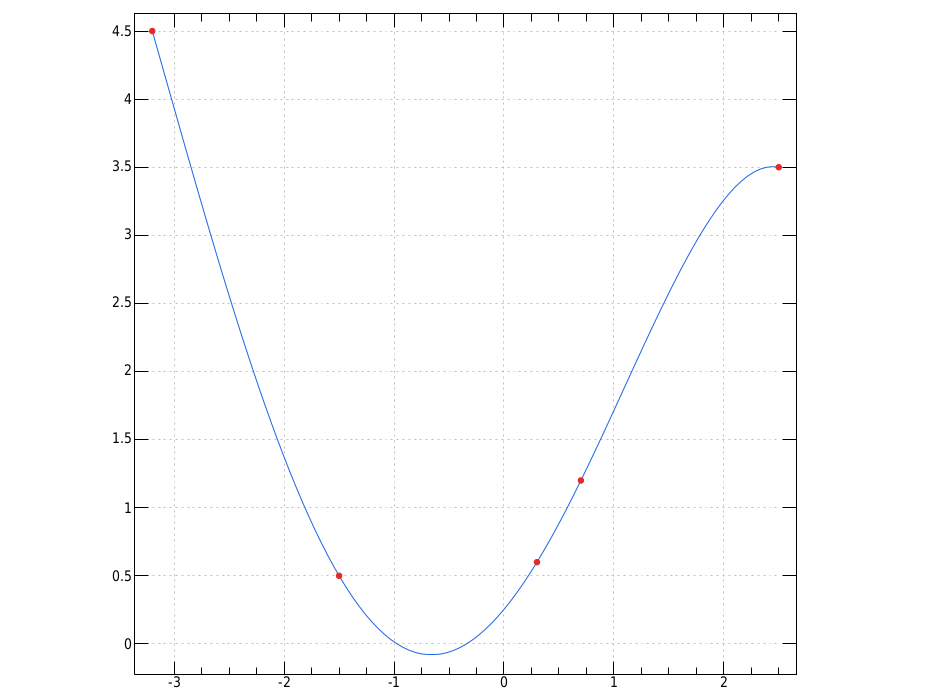
Viewed:

require 'plot'
poly =. VM pts =. _2 ]\ _3.2 4.5 _1.5 0.5 0.3 0.6 0.7 1.2 2.5 3.5
ab =. (<./,>./) {."1 pts
pd 'reset;visible 0'
pd 'type line; color 30 100 230'
pd ab ; 'poly&p.'
pd 'type dot;pensize 1.4; color 230 40 40'
pd <"1 |: pts
pd 'aspect 1'
pd 'show'

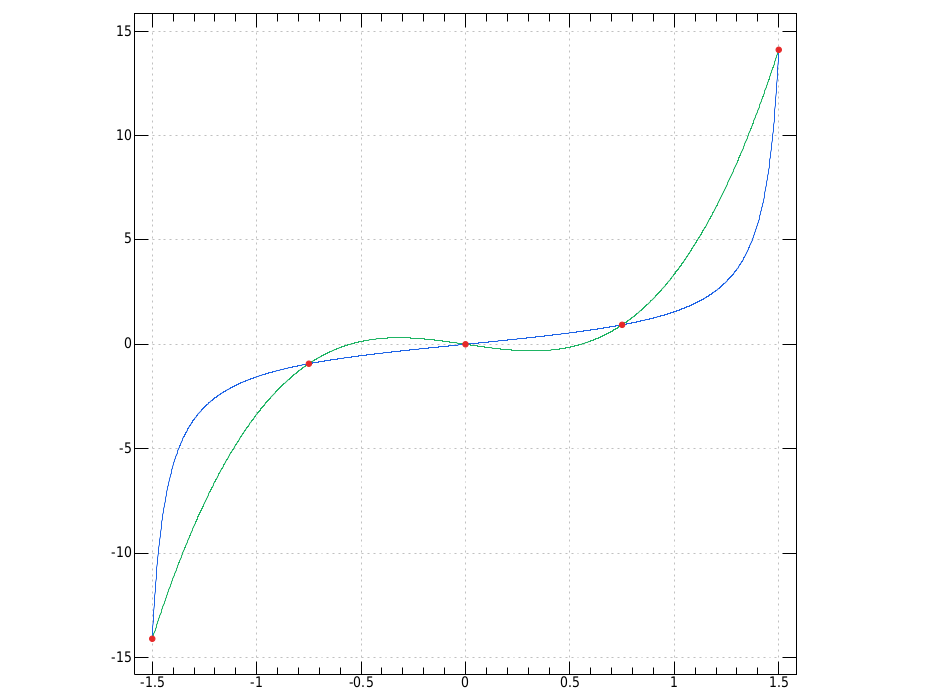
Lagrange

Idea: interpolate by taking polynomials that are 0 at all \(x\) except one, where they equal the corresponding \(y\), then add them up. This is good spot for the infix adverb \.

LG =: +/ @: ({{p.y;~({:x)%(p.1;y)p.{.x}}"1) 1 ]\. {."1
(VM-:LG) _2 ]\ 2 5 3 6 7 4x NB. only 1 way to interpolate!

   LG =: +/ @: ({{p.y;~({:x)%(p.1;y)p.{.x}}"1) 1 ]\. {."1
   (VM-:LG) _2 ]\ 2 5 3 6 7 4x NB. only 1 way to interpolate!
1

Newton

Definitions: Newton basis polynomials are \(n_j(x) = \prod (x-x_i) [0\le i < j]\). Divided differences are \([y_j] = y_j\) and recursively \([y_{a+j}\dots y_a] = \frac{[y_{a+j}\dots y_{a+1}] - [y_{a+j-1},\dots,y_a]}{x_{a+j} - x_a}\) and the Newton Polynomial for interpolating the given points is \(N(x) = \sum a_j n_j(x)[0\le j \le n]\). A good spot to finally try the new fold operators (F::, here).

V =: {{ ((}.-}:) y) % ((-x){.m) - x{.m }} NB. iterate divided differences
A =: {{ ({.y) , y {.F::(x V) i.&.<:#y }} NB. newton coefficients
N =: {{ (xs A {:"1 u) +/ . * 1,*/\ y-}:xs=.{."1 u }} NB. evaluate at y

Viewed:

pd 'reset;visible 0; aspect 1'
pd 'type line; color 30 100 230,30 180 100'
pd (; 3&o.) 3r2 * (%~ i:) 1000
pd (; zs N"0) 3r2 * (%~ i:) 1000
pd 'type dot;pensize 1.4; color 230 40 40'
pd <"1 |: zs
pd 'show'